ALTRO | 2019 | COSTA CORTU' (TN)
Correggere la cosa giusta a volte serve, ma l'importante è saperlo
Leggendo l’ora indicata dagli orologi solari e confrontandola con quella dell’orologio “civile” si trova una certa differenza. Non è sbagliata né l’una né l’altra. Sono due dei tanti modi in cui si suddivide il tempo impiegato dalla Terra a ruotare su se tessa ed al posto dove ci troviamo su di essa. La somma di questi due dati ci consente di paragonare i due orologi.
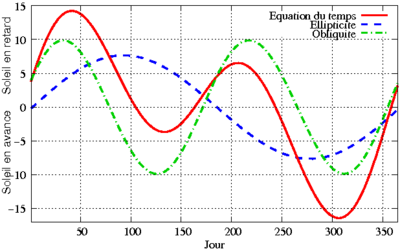
1 – Equazione del tempo: Il grafico (prima foto tratta da Wikipedia) dove in ascisse ci sono i giorni dell’anno ed in ordinate i minuti, mostra in rosso la variazione che è la somma di: in verde dovuta all’obliquità dell’eclittica ed in blu alla differente velocità dovuta all’orbita ellittica attorno al Sole.
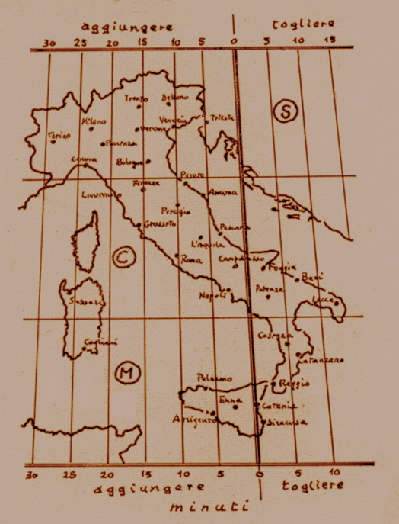
2 – Oltre all’equazione del tempo, anche la nostra posizione sulla Terra influisce sulla lettura degli orologi solari; a Trento il Sole “arriva prima “che a Torino. Conoscendo la longitudine di dove si trova l’orologio solare e sottraendola a quella del meridiano dell’Europa Centrale (15° Est, che passa sull’Etna, foto 2) si calcola la differenza di longitudine. Ogni grado corrisponde a quattro minuti.
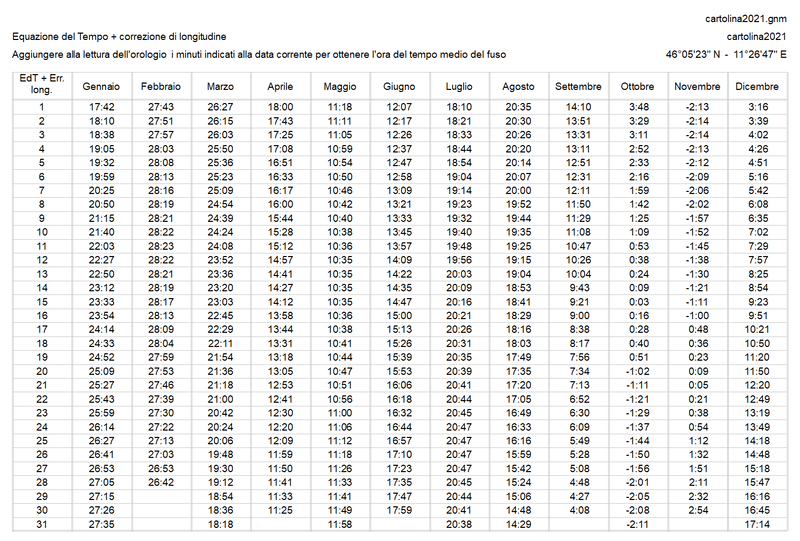
La somma dell’equazione del tempo (linea rossa) e il tempo dovuto alla differenza di longitudine (sempre costante) danno la “correzione”.
Nella tabella della foto 3 la “correzione” per gli orologi solari alla baita delle meridiane.
1 – Equazione del tempo: Il grafico (prima foto tratta da Wikipedia) dove in ascisse ci sono i giorni dell’anno ed in ordinate i minuti, mostra in rosso la variazione che è la somma di: in verde dovuta all’obliquità dell’eclittica ed in blu alla differente velocità dovuta all’orbita ellittica attorno al Sole.
2 – Oltre all’equazione del tempo, anche la nostra posizione sulla Terra influisce sulla lettura degli orologi solari; a Trento il Sole “arriva prima “che a Torino. Conoscendo la longitudine di dove si trova l’orologio solare e sottraendola a quella del meridiano dell’Europa Centrale (15° Est, che passa sull’Etna, foto 2) si calcola la differenza di longitudine. Ogni grado corrisponde a quattro minuti.
La somma dell’equazione del tempo (linea rossa) e il tempo dovuto alla differenza di longitudine (sempre costante) danno la “correzione”.
Nella tabella della foto 3 la “correzione” per gli orologi solari alla baita delle meridiane.